01背包

简单理解 01 背包问题性质

每个物品的数量只有 $1$ 个，选择情况只有选和不选两种，就是 $01$ 背包。

暴力解法时间复杂度为 $O(2^n)$。

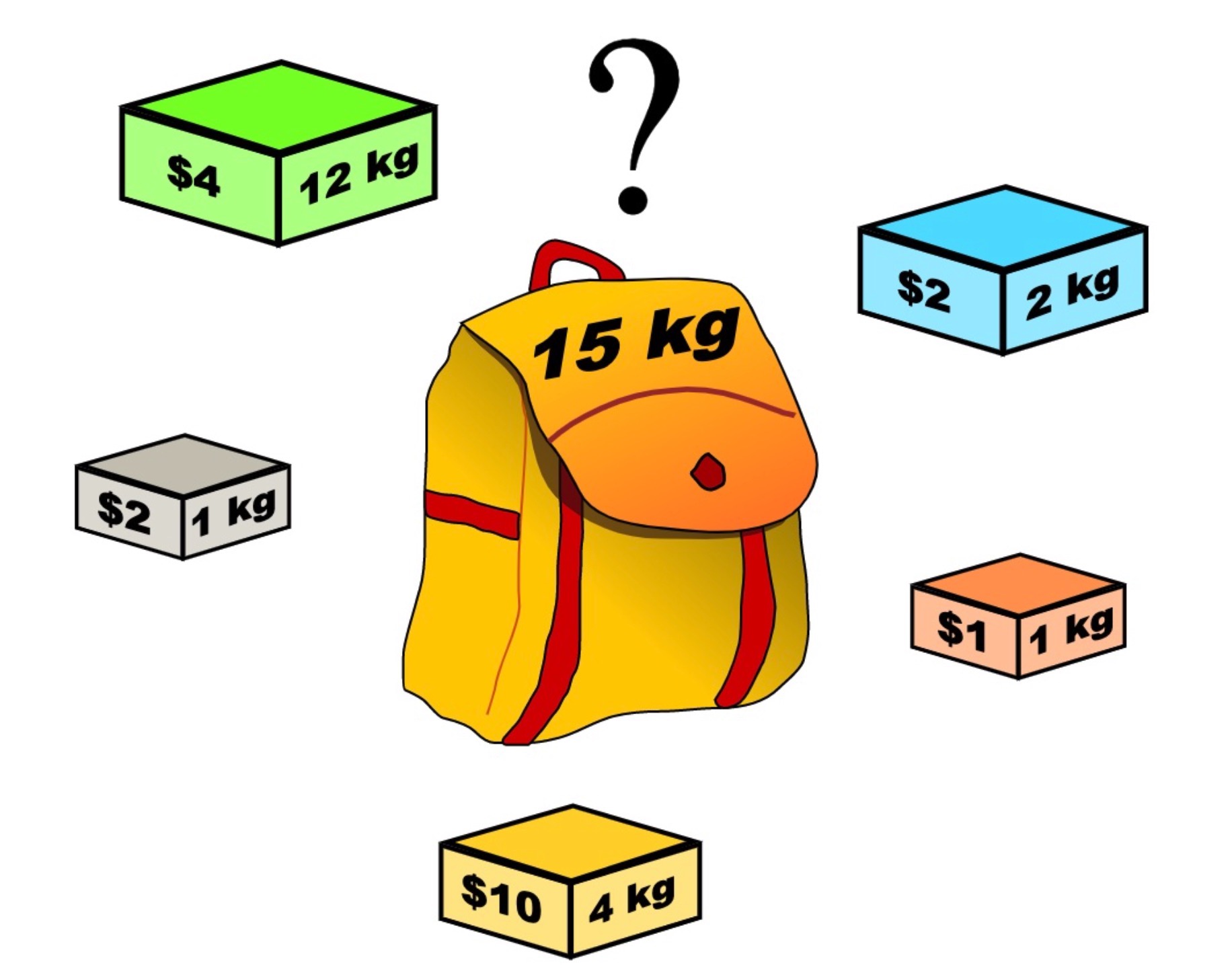
问题描述

一个背包，它最大能收纳的重量为 $packWeight$。

一组物品，每个物品只有一个，第 $i$ 个物品的重量为 $weights[i]$，它的价值为 $values[i]$。

就算背包能容纳的物品的最大价值。

问题分析

总体可以理解为有两个维度的变量

  • 背包容量
  • 物品数量

假设物品共有 $i$ 个，背包的最大收纳重量为 $j$。

那么这个问题的答案就是从这 $i$ 个物品里任意选择若干个放入容量为 $j$ 背包，背包所能收纳的物品的最大价值。

在选择第 $i$ 个物品时，有两种情况（这两种情况是由两种不同的选择方案导致的）：

  • 对前面 $i - 1$ 个物品进行选择后，此时背包的剩余容量不够装下第 $i$ 个物品了（不选择第 $i$ 个物品）。也就是在这种选择方案下，$i$ 个物品和 $i - 1$ 个物品的最大价值是相同的。

  • 剩余容量足够装下第 $i$ 个物品，那么它需要占用 $weights[i]$ 的容量。在这个选择方案中，其余的 $i - 1$ 个物品收纳在 $j - weights[i]$ 容量内（并不一定完全占满）。

二维 dp 数组

可以维护一个二维 $dp$ 数组。

数组下标定义

$i$：在 $0$ ~ $i$ 范围内随意选择物品。

$j$：放入容量为 $j$ 的背包。

$dp[i][j]$：所有可能的选择方案中，物品最大的价值。

递推公式及状态转移方程

通过上述分析，可以知道 $dp[i][j]$ 有两种情况。

递推公式如下：

那么显然，$dp[i][j]$ 应该取两者的最大值。

状态转移方程如下：

初始化 dp 数组

第一种初始化方式

考虑这样一个二维数组的情况

对于第一列，也就是当背包最大容量为 $0$ 的时候，无论怎么选择物品，所能容纳的物品价值都将是 $0$。

所以将第 $1$ 列全部初始化为 $0$。

对于第一行，也就是只从第 1 个物品中选择时，那么只要它的重量小于或等于背包的重量，那么最大价值就是第 1 个物品的重量，否则最大价值就是 0。

所以遍历第 $1$ 行，判断背包容量是否满足第一个物品，初始化对应的值。

1
2
3
4
5
for i := 1; i <= packWeight; i++ {
    if i >= weights[0] {
      dp[0][i] = values[0]
    }
}

这种初始化方式虽然比较直观，但是并没有利用到递推公式，这样的操作看上去使遍历 $dp$ 的过程割裂成了两种方式。

第二种初始化方式

更好的做法是在对整个 $dp$ 数组的赋值过程中，始终使用的是同一种方式。

根据递推公式，第一行的数据值的推导过程为：

那么这样初始化是否可以呢？

1
2
3
for j := 1; j <= packWeight; j++ {
    dp[0][j] = max(dp[0][j], dp[0][j - weights[0]] + values[0])
}

打印一下初始化结果发现是不对的：

但是物品 $0$ 只有一个，第一行的数据应该只有两种可能的值：

  1. 背包重量 $j$ 装不下物品 $0$，初始化为 $0$。
  2. 背包重量 $j$ 可以装下物品 $0$，初始化为 $values[0]$。

但当使用上述方式初始化时，物品会被重复选用。

因为遍历到每一个位置，也就是 $dp[0][j]$ 时，当前位置此时还没有初始化，值是 $0$。所以最终取的结果值就是 $dp[0][j - weights[i]] + values[i]$，而 $dp[0][j - weights[i]]$ 指向的是刚刚已经初始化过的位置的值，再加上当前物品（物品 $0$）的价值。

例如当 $j = 2$ 时：

这是由于递推公式依赖当前位置同行的前面某个位置的值，这就导致了重复。那么可以逆序遍历，这样遍历到当前位置时，它的前面的位置都还没有初始化，就不会导致重复了。

1
2
3
for j := packWeight; j >= 1; j-- {
    dp[0][j] = max(dp[0][j], dp[0][j - weights[0]] + values[0])
}

遍历方式

考虑递推公式的两种情况，对于当前遍历到的位置 $dp[i][j]$，它依赖的数据位置下标为 $i - 1$，$j$ 和 $j - weights[i]$。

都是小于当前位置下标的。

所以利用状态转移方程处理剩余 $dp$ 数组位置时，即可以横向遍历，页可以纵向遍历（横向遍历，也就是先遍历物品选择范围的方式更容易理解）。

举例推导验证

按上述分析的规律举例推导一下 $dp$ 数组，看是否满足。

golang 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
var weights = []int{1, 3, 4}
var values = []int{15, 20, 30}

func max(i, j int) int {
    if i > j {
        return i
    }
    return j
}

func zeroOnePack(packWeight int, weights, values []int) int {
  //初始化
  n := len(weights)
  dp := make([][]int, n)
  for i := 0; i < n; i++ {
      dp[i] = make([]int, packWeight + 1)
  }
  for i := 1; i <= packWeight; i++ {
      if i >= weights[0] {
          dp[0][i] = values[0]
      }
  }
  fmt.Println(dp)

  //计算dp数组的其他位置
  for i := 1; i < n; i++ {
      for j := 1; j <= packWeight; j++ {
          if j < weights[i] {
              dp[i][j] = dp[i - 1][j]
          } else {
              dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weights[i]] + values[i])
          }
      }
  }
  fmt.Println(dp)
  
  return dp[n - 1][packWeight]
}

另一种遍历方式是，当 $j - weights[i]$ 小于 $0$ 时，不做处理。

1
2
3
4
5
6
7
for j := 1; j <= packWeight; j++ {
    for i := 1; i < n; i++ {
        if j >= weights[i] {
            dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weights[i]] + values[i])
        }
    }
}

处理后的结果为：

与上述另一个遍历版本相比，这里差异的几个位置为 $0$ ，这些位置实际是用不上的。

一维 dp 数组

由上述二维 $dp$ 数组观察可知，实际需要的是最后一个元素，并且推导过程是一行一行进行的。

所以实际上只需要维护一行就可以了，遍历推导下一行时直接覆盖到上一行对应的位置，因此维护一个一维 $dp$ 数组就可以了。

整体思路与二维 $dp$ 数组时一致的，简单列举一下数据变化过程帮助理解：

维护一个一维数组

与二维 $dp$ 数组同样的初始化

遍历处理物品 $1$ 时，不再是二维数组的第二行，而是直接覆盖在这个一维 $dp$ 数组上

遍历处理物品 $2$

golang 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
func zeroOnePack(packWeight int, weights, values []int) int {
  //初始化
  n := len(weights)
  dp := make([]int, packWeight + 1)
  for i := 1; i <= packWeight; i++ {
      if i >= weights[0] {
          dp[i] = values[0]
      }
  }
  fmt.Println(dp)

  //计算dp数组的其他位置
  for i := 1; i < n; i++ {
      for j := 1; j <= packWeight; j++ {
          if j >= weights[i] {
              dp[j] = max(dp[j], dp[j - weights[i]] + values[i])
          }
      }
  }
  fmt.Println(dp)

  return dp[packWeight]
}

这个实现是有问题的，只是对于这个示例来说，可以通过。

使用一维 $dp$ 数组，实际上就要考虑采用上述第二种初始化方式时遇到的问题，会发生重复选择物品的情况。

来看这样一个例子：

初始状态：

初始化后：

第 $2$ 行：

第 $3$ 行：

显然在最后一个单元格发生了重复，正常是不可能出现 $4$ 的。

这是因为 $j = 4$ 时：

而 $dp[2]$ 位置就已经选择了物品 $1$，$dp[4]$ 在 $dp[2]$ 的基础上又重复选择了一次。

在使用二维 $dp$ 数组时不会发生这种情况，因为遍历下一行时不会去覆盖上一行的数据。

那么这里为了不发生重复，就要使用在第二种初始化方式中讨论过的技巧，逆序遍历。

在逆序情况下，正确的情况应该是，在遍历 $dp[4]$ 时，$dp[2]$ 的是 $1$ 而不是 $2$ （这就是在问题分析中说的：选物品 $1$ 时，扣除物品 $1$ 的重量以外，剩余的背包重量在除物品 $1$ 以外剩余可选的物品中，能选择的最大值。此时剩余的重量并不一定会装满。）：

第 $2$ 行：

第 $3$ 行：

golang代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
func zeroOnePack(packWeight int, weights, values []int) int {
  //初始化
  n := len(weights)
  dp := make([]int, packWeight + 1)
  for j := packWeight; j >= weights[0]; j-- {
    dp[j] = max(dp[j], dp[j - weights[0]] + values[0])
  }
  fmt.Println(dp)

  //计算dp数组的其他位置
  for i := 1; i < n; i++ {
      for j := packWeight; j >= weights[i]; j-- {
          dp[j] = max(dp[j], dp[j - weights[i]] + values[i])
      }
  }
  fmt.Println(dp)

  return dp[packWeight]
}

扫一扫，分享到微信

微信分享二维码

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

曾经是个修理工，<br>现在是一枚码农。<br>路漫漫其修远兮，<br>吾将上下而求索。<br>