完全背包

2021-07-19

理解完全背包的性质

在 $01$ 背包问题中，每一个物品的数量只有一个（也就是说每个物品只能选择一次）。

而当每个物品的数量有 $N$ 个（也就是对于同一重量、同一价值的物品可以多次选择）时，这就是一个完全背包的问题。

问题描述

把 $01$ 背包问题稍作修改就成为了完全背包问题。

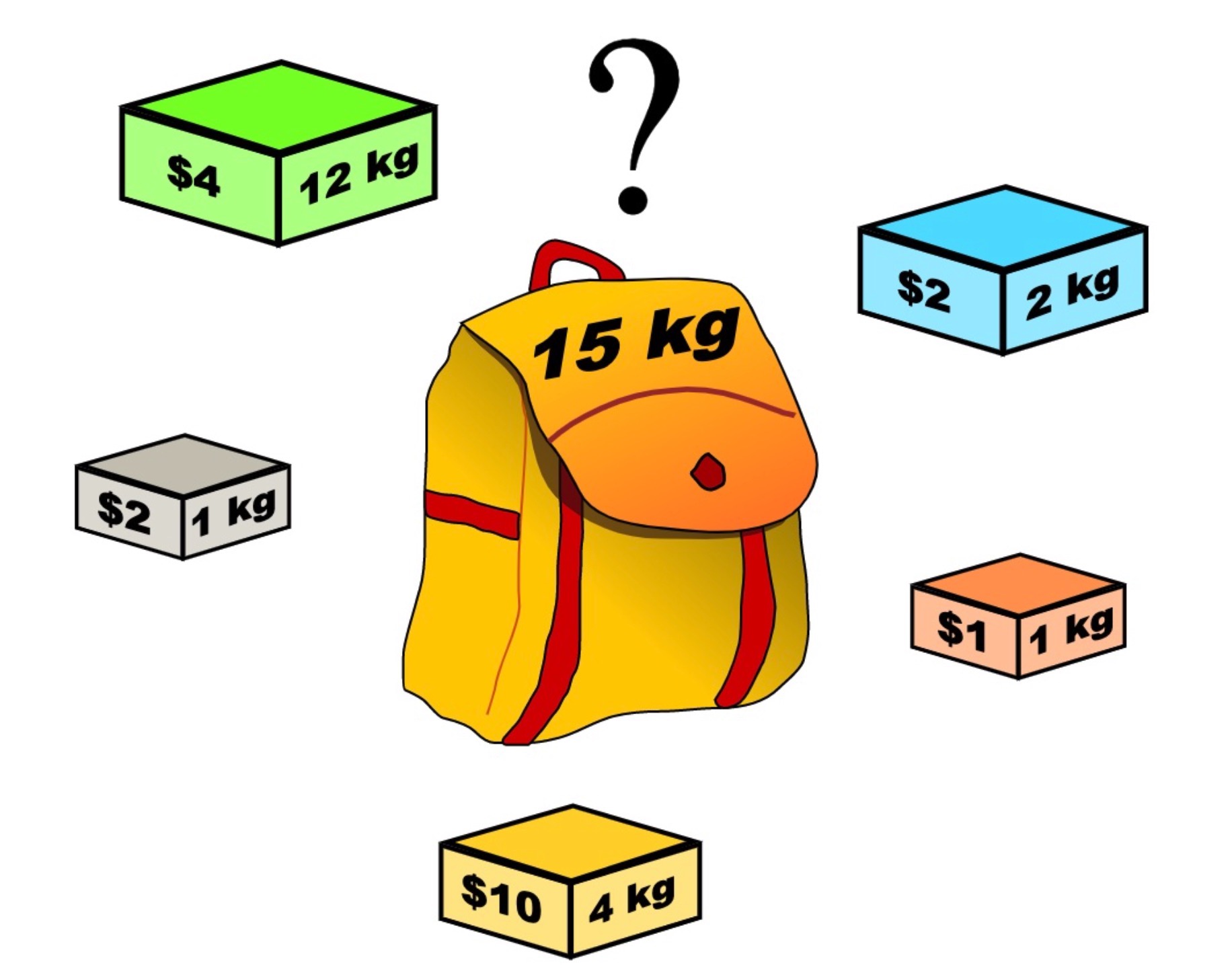
一个背包，它最大能收纳的重量为 $bagWeight$。

一组物品，每个物品有无数个（可以重复选择），第 $i$ 个物品的重量为 $weights[i]$，它的价值为 $values[i]$。

求背包能容纳的物品的最大价值。

$示例\ \ \ \begin{array}{|c|c|c|c|} \hline bagWeight&4\\ \hline weights&1&3&4\\ \hline values&15&20&30\\ \hline \end{array}$

问题分析

在 $01$ 背包问题中，为了防止物品被重复选择，内层循环采用了逆序遍历。

但是在完全背包问题中，可以重复选用物品，所以将内层循环改为正序遍历就可以了。

二维 $dp$ 数组

这里 $dp$ 数组下标定义与 $01$ 背包是相同的。

$dp[i][j]$ 表示从下标为 $0$ ~ $i$ 的物品中任意选，背包最大容量为 $j$ 时，背包能容纳的最大重量。

完全背包中 $dp[i][j]$ 同样可以从两种情况得到：

$dp[i][j] = \begin{cases} dp[i - 1][j]\\ dp[i][j - weights[i]] + values[i] \end{cases}$

第一种情况，假设此时背包剩余容量已无法容纳物品 $i$。背包最大容量为 $j$，从下标为 $0$ ~ $i$ 的物品中任意选择物品得到的物品最大价值，与背包最大容量为 $j$，从下标为 $0$ ~ $i - 1$ 的物品中任意选择物品得到的物品最大价值是相同的。

第二种情况，假设背包剩余容量可以容纳物品 $i$。显然把它放进背包需要消耗 $weights[i]$ 的容量，也就是扣除一个物品 $i$ 的重量后，背包剩余容量为 $j - weights[i]$，则从下标为 $0$ ~ $i$ 的物品中任意选择物品，最大容量为 $j - weights[i]$ 的背包能容纳的物品最大价值就是 $dp[i][j - weights[i]]$，然后再加上一个刚刚被暂时扣除的物品 $i$ 的价值。

直接列举一下 $dp$ 数组的推导过程：

初始状态

$\begin{array}{|c|c|c|c|c|c|} \hline &重量0&重量1&重量2&重量3&重量4\\ \hline 物品0\\ \hline 物品1\\ \hline 物品2\\ \hline \end{array}$

初始化 $dp$ 数组后，背包最大重量为 $0$ 时，能容纳的物品最大价值必然是 $0$。

$\begin{array}{|c|c|c|c|c|c|} \hline &重量0&重量1&重量2&重量3&重量4\\ \hline 物品0&0\\ \hline 物品1&0\\ \hline 物品2&0\\ \hline \end{array}$

遍历物品 $0$ （物品可以重复选择了，遍历完物品 $0$ 后，第一行数据与 $01$ 背包明显不同）

$\begin{array}{|c|c|c|c|c|c|} \hline &重量0&重量1&重量2&重量3&重量4\\ \hline 物品0&0&15&30&45&60\\ \hline 物品1&0\\ \hline 物品2&0\\ \hline \end{array}$

遍历物品 $1$

$\begin{array}{|c|c|c|c|c|c|} \hline &重量0&重量1&重量2&重量3&重量4\\ \hline 物品0&0&15&30&45&60\\ \hline 物品1&0&0&0&45&60\\ \hline 物品2&0\\ \hline \end{array}$

遍历物品 $2$

$\begin{array}{|c|c|c|c|c|c|} \hline &重量0&重量1&重量2&重量3&重量4\\ \hline 物品0&0&15&30&45&60\\ \hline 物品1&0&0&0&45&60\\ \hline 物品2&0&0&0&0&60\\ \hline \end{array}$

golang 代码实现

func max(i, j int) int {
    if i > j {
        return i
    }
    return j
}

var (
  weights = []int{1, 3, 4}
  values = []int{15, 20, 30}
)

func completePack(packWeight int, weights, values []int) int {
    dp := make([][]int, len(weights))
    for i, _ := range dp {
        dp[i] = make([]int, packWeight + 1)
    }
    fmt.Println("初始化前: ", dp)

    for j := 1; j <= packWeight; j++ {
        dp[0][j] = dp[0][j - weights[0]] + values[0]
    }
    fmt.Println("初始化后: ", dp)

    //遍历物品
    for i := 1; i < len(weights); i++ {
        //遍历背包
        for j := 1; j <= packWeight; j++ {
            if j >= weights[i] {
                dp[i][j] = max(dp[i - 1][j], dp[i][j - weights[i]] + values[i])
            }
        }
        fmt.Println(dp)
    }
    return dp[len(weights) - 1][packWeight]
}

$dp$ 数组的遍历顺序与 $01$ 背包也是相同的。先遍历物品或先遍历背包都是可以的。

一维 $dp$ 数组

同样与 $01$ 背包问题中的一维 $dp$ 数组相似，不再详细分析，先记录一下代码实现。

func completePack(packWeight int, weights, values []int) int {
    dp := make([]int, packWeight + 1)
    fmt.Println("初始化前: ", dp)

    //遍历物品
    for i := 0; i < len(weights); i++ {
        //遍历背包
        for j := 1; j <= packWeight; j++ {
            if j >= weights[i] {
                dp[j] = max(dp[j], dp[j - weights[i]] + values[i])
            }
        }
        fmt.Println(dp)
    }
    return dp[packWeight]
}

在 $01$ 背包问题中，一维 $dp$ 数组的遍历过程必须在外层循环遍历物品，内层循环遍历背包容量，而在完全背包（指纯完全背包，本题就是一个纯完全背包问题）中，先遍历物品和先遍历背包容量是一样的。

总结

纯完全背包问题与纯 $01$ 背包问题的差别：

在分析问题时，可以理解为物品是不是可以重复选择（每个物品有多件）
在代码实现中，可以理解为对背包容量的遍历方向（完全背包是正序（从小到大）遍历背包容量，而 $01$ 背包是逆序（从大到小）遍历背包容量）。